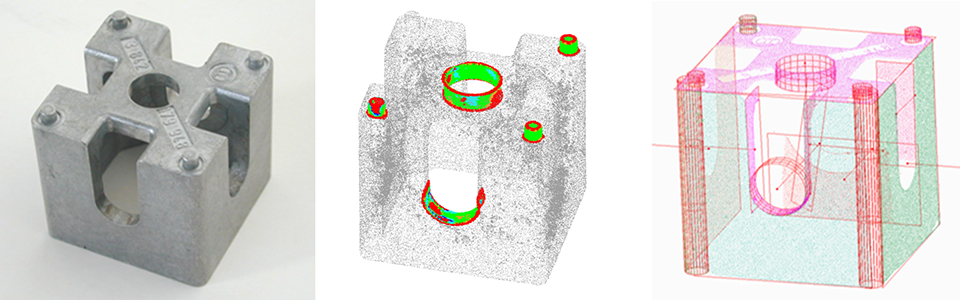
Fit methods

Fitting curves and surfaces into measuring points is a key aspect of many tasks in industrial image processing and coordinate measuring technology. The fitting of geometric elements is also important in object recognition and scene analysis.

In the department “Machine Vision and Signal Processing”, methods have been developed to fit geometric curves, such as circles or ellipses, as well as basic geometric primitives, such as planes, cylinders, spheres, cones or Tori. These are based on the least squares method (often known as Gaussian fitting), which enables any element that can be described parametrically or implicitly to be fitted. The method also includes segmentation, which automatically excludes all points that do not belong to the object from the fitting process. Besides fitting individual basic geometric primitives, algorithms have also been developed to fit combined geometric primitives, such as concentric cylinders or elongated holes in the form of 3D objects.

The department has also developed its own best-fit method for fitting STL models (triangulated CAD models) into point clouds.

The Gaussian fitting method is not suitable for all applications. Especially in coordinate measuring technology, the Tschebyscheff best-fit method as well as circumscribed or inscribed features are also used. The department also has some of its own best-fit algorithms based on Tschebyscheff and Minimum Zone fits.